
Diffraction gratings are manufactured either classically with the use of a ruling engine, or holographically with the use of interference fringes generated at the intersection of two laser beams.
Diffraction gratings are manufactured either classically with the use of a ruling engine by burnishing grooves with a diamond stylus, or holographically with the use of interference fringes generated at the intersection of two laser beams1.
Classically ruled gratings may be planar or concave and possess grooves, each parallel with the next. Holographic grating grooves may be either parallel or of unequal distribution in order to optimize system performance. Holographic gratings are generated on planar, spherical, toroidal, and many other surfaces.
Regardless of the shape of the surface or whether classically ruled or holographic, the text that follows is applicable to each; explanations are provided where there are differences.
Diffraction gratings are manufactured either classically with the use of a ruling engine, or holographically with the use of interference fringes generated at the intersection of two laser beams.
Grating Equations: Definitions and Units
Before introducing the basic equations, a brief explanation on monochromatic light and continuous spectra must first be presented.
Monochromatic light has infinitely narrow spectral width. Good sources which approximate such light include single mode lasers and very low pressure, cooled spectral calibration lamps. These are also variously known as “line” or “discrete line” sources.
A continuous spectrum has finite spectral width, e.g. “white light.” In principle, all wavelengths are present, but in practice a “continuum” is almost always a segment of a spectrum. Sometimes a continuous spectral segment may be only a few parts of a nanometer wide and resemble a line spectrum.
The equations that follow are for systems in air where μ0 = 1. Therefore, λ = λ0 = wavelength in air.
λ0 = λ/μ0
1 nm = 10-6 mm
1 μm = 10-3 mm
1 Å = 10-7 mm
The most fundamentals grating equations is given by: (1) sinα + sinβ = 10-6 knλ
In most monochromators, the location of the entrance and exit slits are fixed, and the grating rotates around a plane through the center of its face. The angle, DV, is, therefore, a constant.
In most monochromators, the location of the entrance and exit slits are fixed, and the grating rotates around a plane through the center of its face. The angle, DV, is, therefore, a constant determined by:
(2) DV = β-α
Monochromator Configuration.
If the value of α and β is to be determined for a given wavelength (1), the grating equation may be expressed as:
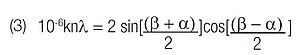
Assuming the value of DV is known, α and β may be determined through Equations (2) and (3) (see Fig. 2 and Fig. 3).
Spectrograph Configuration.
LA = Entrance arm length
LB = Exit arm length at λn
βH = Angle between the perpendicular to the spectral plane and the grating normal
LH = Perpendicular distance from the spectral plane to grating.
Table 1 shows how the angle of incidence and angle of diffraction vary depending on the deviation angle for a 1200 g/mm grating set to diffract 500 nm in a monochromator geometry.
Table 1 shows how α and β vary depending on the deviation angle for a 1200 g/mm grating set to diffract 500 nm in a monochromator geometry, based on Fig. 2.
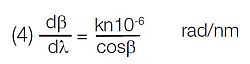
dβ = angular separation between two wavelengths (radians)
dλ = differential separation between two wavelengths (nm)
Linear dispersion defines the extent to which a spectral interval is spread out across the focal field of a spectrometer and is expressed in nm/mm, Å/mm, cm-1/mm, etc. For example, consider two spectrometers: one instrument disperses a 0.1 nm spectral segment over 1 mm while the other takes a 10 nm spectral segment and spreads it over 1 mm.
It is easy to imagine that fine spectral detail would be more easily identified in the first instrument than the second. The second instrument demonstrates “low” dispersion compared to the “higher” dispersion of the first. Linear dispersion is associated with an instrument’s ability to resolve fine spectral detail.
Linear dispersion perpendicular to the diffracted beam at a central wavelength, λ, is given by:
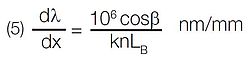
where LB is the effective exit focal length in mm and dx is the unit interval in mm along the focal field (see Fig. 2).
In a monochromator, LB is the arm length from the focusing mirror to the exit slit, or if the grating is concave, from the grating to the exit slit. Linear dispersion, therefore, varies directly with cos β, and inversely with the exit path length, LB, diffraction order (k), and groove density, n.
In a spectrograph, the linear dispersion for any wavelength other than the wavelength which is normal to the spectral plane will be modified by the cosine of the angle of inclination or tilt angle (γ) at wavelength λn. Fig. 3 shows a “flat field” spectrograph as used with a linear diode array.
Linear Dispersion
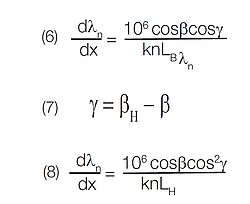
A first order spectrum from 200 to 1000 nm spread over a focal field in spectrograph configuration.
Fig. 4 shows a first order spectrum from 200 to 1000 nm spread over a focal field in spectrograph configuration. From Equation (1) with a grating of given groove density and for a given value of α and β:
(9) kλ = constant
so that if the diffraction order k is doubled, λ is halved, etc.
If, for example, a light source emits a continuum of wavelengths from 20 nm to 1000 nm, then at the physical location of 800 nm in first order (Fig. 4) wavelengths of 400, 266.6, and 200 nm will also be present and available to the same detector. In order to monitor only light at 800 nm, filters must be used to eliminate the higher orders.
First order wavelengths between 200 and 380 nm may be monitored without filters because wavelengths below 190 nm are absorbed by air. If, however, the instrument is evacuated or N2 purged, higher order filters would again be required.
Resolving “power” is a theoretical concept and is given by:
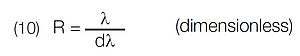
where, dλ is the difference in wavelength between two spectral lines of equal intensity. Resolution is then the ability of the instrument to separate adjacent spectral lines. Two peaks are considered resolved if the distance between them is such that the maximum of one falls on the first minimum of the other. This is called the Rayleigh criterion.
It may be shown that:
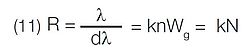
λ = the central wavelength of the spectral line to be resolved
Wg= the illuminated width of the grating
N = the total number of grooves on the grating
The numerical resolving power “R” should not be confused with the resolution or bandpass of an instrument system.
Theoretically, a 1200 g/mm grating with a width of 110 mm that is used in first order has a numerical resolving power R = 1200 × 110 = 132,000. Therefore, at 500 nm, the bandpass is equal to:
dλ= 500/132,000 = 0.0038 nm
In a real instrument, however, the geometry is fixed by (1).
Solving for k:
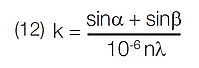
But the ruled width, Wg, of the grating:
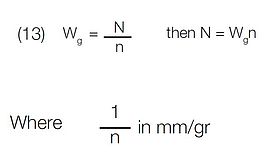
After substitution of (12) and (13) in (11), resolving power may also be expressed as:
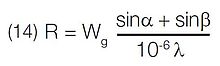
Consequently, the resolving power of a grating is dependent on:
Because bandpass is also determined by the slit width of the spectrometer and residual system aberrations, an achieved bandpass at this level is only possible in diffraction limited instruments, assuming an unlikely 100% of theoretical.
Blaze is defined as the concentration of a limited region of the spectrum into any order other than the zero order. Blazed gratings are manufactured to produce maximum efficiency at designated wavelengths. A grating may, therefore, be described as “blazed at 250 nm” or “blazed at 1 micron,” etc. by appropriate selection of groove geometry.
A blazed grating is one in which the grooves of the diffraction grating are controlled to form right triangles with a “blaze angle, ω,” as shown in Fig. 5. However, apex angles up to 110° may be present especially in blazed holographic gratings. The selection of the peak angle of the triangular groove offers opportunity to optimize the overall efficiency profile of the grating.
Blazed grating groove profiles are calculated for the Littrow condition where the incident and diffracted rays are in auto collimation.
Blazed grating groove profiles are calculated for the Littrow condition where the incident and diffracted rays are in auto collimation (i.e., α = β). The input and output rays, therefore, propagate along the same axis. In this case, at the “blaze” wavelength λB.
For example, the blaze angle (ω) for a 1200 g/mm grating blazed at 250 nm is 8.63° in first order (k = 1).
Typical efficiency curve of a blazed, ruled grating.
Unless otherwise indicated, the efficiency of a diffraction grating is measured in the Littrow configuration at a given wavelength.
Typical efficiency curves of a non-blazed, holographic grating.
Relative efficiency measurements require the mirror to be coated with the same material and used in the same angular configuration as the grating.
See Fig. 6 and Fig. 7 for typical efficiency curves of a blazed, ruled grating, and a non-blazed, holographic grating, respectively.
As a general approximation, for blazed gratings the strength of a signal is reduced by 50% at two-thirds the blaze wavelength, and 1.8 times the blaze wavelength.
A grating blazed in first order is equally blazed in the higher orders. Therefore, a grating blazed at 600 nm in first order is also blazed at 300 nm in second order, and so on.
Efficiency in higher orders usually follows the first order efficiency curve. For a grating blazed in first order, the maximum efficiency for each of the subsequent higher orders decreases as the order k increases.
The efficiency also decreases the farther away from Littrow conditions in which the grating is used (e.g. α ≠ β). Holographic gratings may be designed with groove profiles that discriminate against high orders. This may be particularly effective in the UV and VIS using laminar groove profiles created by ion etching.
Note: Just because a grating is “non-blazed” does not necessarily mean that it is less efficient! See Fig. 7 showing the efficiency curve for an 1800 g/mm sinusoidal grooved holographic grating.
Light other than the wavelength of interest reaching a detector (often including one or more elements of “scattered light”) is referred to as stray light.
Scattered light may be produced by either of the following:
Holographic gratings show no ghosts because there are no periodic ruling errors and, therefore, often represent the best solution to ghost problems.
If the diffraction grating has periodic ruling errors, a ghost, which is not scattered light, will be focused in the dispersion plane. Ghost intensity is given by:
![]()
where,
IG = ghost intensity
IP = parent intensity
n = groove density
k = order
e = error in the position of the grooves
Ghosts are focused and imaged in the dispersion plane of the monochromator.Stray light of a holographic grating is usually up to a factor of ten times less than that of a classically ruled grating, is typically non-focused, and when present, radiates through 2π steradians.
Holographic gratings show no ghosts because there are no periodic ruling errors and, therefore, often represent the best solution to ghost problems.
Remember, ghosts and subsequent stray light intensity are proportional to the square of order and groove density (n2 and k2 from Equation (17). Beware of using ruled gratings in high order or with high groove density.